[탐색 알고리즘] 값 탐색 - 선형탐색, 이분탐색
탐색 알고리즘은 원하는 데이터를 찾는 기본적인 방법이다. 배열에서는 선형 탐색과 이분 탐색이, 그래프와 트리에서는 DFS와 BFS가 대표적이다. 이 글에서는 특히 값 탐색에 초점을 맞춰 선형 탐색과 이분 탐색의 개념, 복잡도, STL 활용법을 정리한다.
![[탐색 알고리즘] 값 탐색 - 선형탐색, 이분탐색](/content/images/size/w2000/2025/09/photo-1510511459019-5dda7724fd87-2.jpg)
탐색이란?
탐색 알고리즘은 말 그대로 원하는 데이터(값 또는 노드)를 찾는 방법이다. 프로그래밍에서는 크게 두 가지 상황에서 탐색이 필요하다.
- 배열 또는 리스트에서 값 찾기
-> 선형 탐색 (Linear Search) / 이분 탐색 (Binary Search) - 트리 또는 그래프 구조에서 노드 찾기
-> 깊이 우선 탐색 (DFS, Depth-First Search) / 너비 우선 탐색 (BFS, Breadth-First Search)
선형 탐색 (Linear Search)
탐색 방법
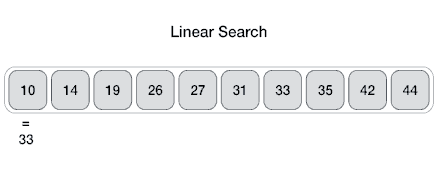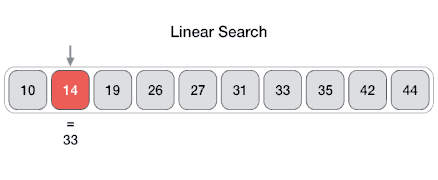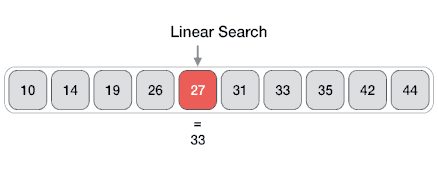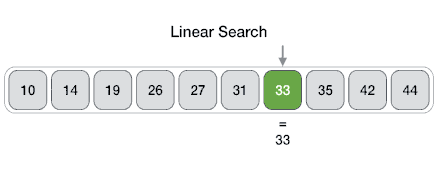
배열에 있는 값들을 처음부터 끝까지 차례대로 비교하며 값을 찾는 탐색 방법이다. 이분 탐색과는 다르게 정렬이 되어 있을 필요가 없다.
종료 조건
n개의 배열에 있어서 특정 값을 찾는다면, 인덱스 n부터 n-1까지 순회하며 arr[i] == target이 되면 종료한다. 찾지 못한 채로 인덱스가 끝까지 간다면 그대로 종료한다.
복잡도
최악의 경우에 찾고자 하는 값이 배열의 마지막에 있는 경우는 n번 순회할 것이다. 반대로 최선의 경우에는 찾고자 하는 값이 배열의 처음에 있는 경우일 것이다. 따라서 복잡도는 다음과 같다.
- 최악/평균
O(n) - 최선
O(1)
샘플 코드
#include <vector>
int linearSearch(const std::vector<int> &arr, int target)
{
for (std::size_t i = 0; i < arr.size(); ++i)
{
if (arr[i] == target)
{
return static_cast<int>(i);
}
}
return -1;
}이분 탐색 (Binary Search)

탐색 방법
배열 내에서 매 단계 검색 구간을 절반으로 줄이는것을 반복하며 값을 찾는다. 단, 선형 탐색과는 달리 반드시 배열이 정렬되어 있어야 한다.
- 정렬된 배열에서 시작과 끝 인덱스를 잡는다.
- 가운데 인덱스를 구해 목표 값과 비교한다.
- 같으면 찾은 것이고, 작으면 오른쪽, 크면 왼쪽 구간만 남긴다.
이 과정을 값이 나올 때까지 반복한다.
종료 조건
- 가운데 값이 목표 값과 같을 때 탐색을 종료한다.
- 시작 인덱스가 끝 인덱스를 넘어가면 배열에 값이 없다고 종료한다.
복잡도
찾고자 하는 값이 배열의 가운데에 바로 있는 경우에는 한 번의 비교만으로 탐색이 끝난다. 반대로 찾고자 하는 값이 배열에 없거나, 가장 왼쪽이나 오른쪽 끝에 위치한 경우에는 탐색 구간을 계속 반으로 줄여가며 끝까지 확인해야 한다. 이때 탐색 횟수는 배열의 크기를 2로 나눌 수 있을 만큼 반복되며, 이는 대략 log₂(n) 번이다.
따라서 복잡도는 다음과 같다.
- 최악/평균: O(log n)
- 최선: O(1)
샘플 코드
#include <vector>
int binarySearch(const std::vector<int> &arr, int target)
{
if (arr.empty())
{
return -1;
}
int left = 0;
int right = static_cast<int>(arr.size()) - 1;
while (left <= right)
{
int mid = left + (right - left) / 2;
if (arr[mid] == target)
{
return mid;
}
else if (arr[mid] < target)
{
left = mid + 1;
}
else
{
right = mid - 1;
}
}
return -1;
}
값 탐색 관련 STL
값 탐색 알고리즘을 실무에서 직접 구현하는 경우는 드물 것이다. 이미 STL에서 최적화된 알고리즘을 제공해주고 있기 때문이다.
선형 탐색
| 함수 | 헤더 | 설명 |
|---|---|---|
std::find(first, last, value) |
<algorithm> |
[first, last) 구간에서 value와 같은 원소를 처음 찾는다. 없으면 last 반환 |
std::find_if(first, last, pred) |
<algorithm> |
조건자 pred를 만족하는 첫 번째 원소를 찾는다 |
std::find_if_not(first, last, pred) |
<algorithm> |
조건자 pred를 만족하지 않는 첫 번째 원소를 찾는다 |
이 함수들은 값이나 존재 여부가 아니라 iterator(반복자)를 반환한다. iterator는 "컨테이너 안에서 원소를 가리키는 포인터 비슷한 것"이라고 이해하면 된다. 따라서 실제 값을 가져오고 싶다면 *it 처럼 역참조 연산자(*)를 붙이면 된다
std::find
지정한 값과 같은 원소를 선형 탐색으로 찾는다. 못 찾으면 last iterator를 반환한다.
#include <algorithm>
#include <vector>
// vector<int> 내에 원소 n이 있는지
bool isExists(const std::vector<int> &array, int n)
{
auto it = std::find(array.begin(), array.end(), n);
return it != array.end();
}
int main()
{
std::vector<int> array{1, 2, 3, 4, 5};
isExists(array, 5); // true
isExists(array, 10); //false
}std::find_if
주어진 조건자(pred)를 만족하는 첫 번째 원소를 찾는다. 조건은 보통 람다로 작성한다.
#include <algorithm>
#include <vector>
int findFirstEvenNumber(const std::vector<int> &array)
{
auto it = std::find_if(array.begin(), array.end(), [](int num)
{ return num % 2 == 0; });
// 첫 번째로 발견된 짝수 원소를 반환하고 없으면 -1을 반환
return it != array.end() ? *it : -1;
}
int main()
{
std::vector<int> array{1, 2, 3, 4, 5};
auto even_num = findFirstEvenNumber(array);
std::cout << "even num: " << even_num << "\n"; // 2
}이분 탐색 (선 정렬 필요)
| 함수 | 헤더 | 설명 |
|---|---|---|
std::binary_search(first, last, value) |
<algorithm> |
value가 구간에 존재하는지 여부만 true/false 반환 |
std::lower_bound(first, last, value) |
<algorithm> |
value 이상(>=)이 처음 나오는 위치 반환 |
std::upper_bound(first, last, value) |
<algorithm> |
value 초과(>)가 처음 나오는 위치 반환 |
std::equal_range(first, last, value) |
<algorithm> |
[lower_bound, upper_bound) 쌍 반환 (중복 구간 한 번에 처리) |
std::binary_search
std::binary_search(first, last, value) 는 정렬된 구간에서 value가 존재하면 true, 없으면 false를 반환한다. 반환 타입이 bool이므로 단순히 "있다/없다" 판정에 쓰기 좋다. 함수 명처럼, 내부적으로는 이분 탐색 알고리즘을 사용한다.
#include <algorithm>
#include <vector>
bool isExistsBinary(const std::vector<int> &array, int n)
{
// array는 반드시 정렬되어 있어야 한다.
return std::binary_search(array.begin(), array.end(), n);
}
int main()
{
std::vector<int> sorted_array{1, 3, 5, 7, 9};
bool result1 = isExistsBinary(sorted_array, 5); // true
bool result2 = isExistsBinary(sorted_array, 2); // false
}std::lower_bound & std::upper_bound
std::lower_bound | std::upper_bound 는 값 존재 여부 + 인덱스를 얻을 수 있다. 값이 없을 때는 "삽입할 위치"를 알려준다. 따라서 탐색 + 삽입 위치 결정이 필요한 경우(예: 정렬된 배열 유지)에서 매우 유용하다.
#include <algorithm>
#include <vector>
// 삽입 위치 찾기 예
int getInsertPosition(const std::vector<int> &array, int n)
{
auto it = std::lower_bound(array.begin(), array.end(), n);
return static_cast<int>(std::distance(array.begin(), it));
}
int main()
{
std::vector<int> sorted_array{1, 3, 5, 7, 9};
int pos1 = getInsertPosition(sorted_array, 4); // 2 (3과 5 사이)
int pos2 = getInsertPosition(sorted_array, 10); // 5 (맨 뒤)
}
요약
| 구분 | 선형 탐색 (Linear Search) | 이분 탐색 (Binary Search) |
|---|---|---|
| 전제 조건 | 정렬 여부 상관 없음 | 정렬된 배열이어야 함 |
| 동작 방식 | 처음부터 끝까지 순서대로 비교 | 중간값과 비교 → 절반씩 탐색 구간 줄이기 |
| 시간 복잡도 | 최악/평균 O(n)최선 O(1) | 최악/평균 O(log n)최선 O(1) |
| 구현 난이도 | 매우 간단 | 경계 처리 주의 필요 |
| 장점 | 어디서든 적용 가능, 직관적 | 탐색 속도 빠름, 큰 데이터에 적합 |
| 단점 | 데이터가 크면 느림 | 정렬 비용 필요, 구현 실수 위험 |